where:

F = the effective DOF of the assembly or mechanism

l = the DOF of the space in which the mechanism operates (for spatial motion l  = 6, and for motion in a plane or on a surface l = 3)

l = number of links

j = number of joints

f_i = Degrees-Of-Freedom of i-th joint

I_d = idle or passive Degrees-Of-Freedom

There are special geometrical conditions that have to be taken into account in the determination of the DOF. For instance, one shaft with both ends fixed with ball joints has one idle DOF, and that is rotation about the axis that passes through both of the joints. The term I_d takes care of these cases. We are considering an SPFA, with n links, when all actuators are fixed. Referring to Figure 2, we have l = 6 for spatial motion, l = n + 1+1 for six links, platform and base, j = 2·n as the number of mobile joints in the mechanism. If the ball-and-socket joints are used, then f_i = 3, since every such a jo int has three degrees of freedom. Each link connects rigidly two ball-and-socket joints, so that we have I_d= n idle degrees of freedom. Equation ( 23 ) evaluates to:

Instead of ball-and-socket joints, universal joints can be used with an addition of a cylindrical joint positioned somewhere along the each link. Then we have l = 6 for spatial motion, l = n + 1+1 = 8 for six links, platform and base, j = 3·n as the number of mobile joints in the mechanism. There are twelve universal joints each having two degrees of freedom (f_i = 2 , for i=1,..,2n) and six cylindrical joints each having one degree of freedom (f_i = 1, for i= 2n +1,.., 3n), and there are no idle degrees of freedom in the mechanism, I_d = 0. In this case, equation ( 23 ) gives:

Equations ( 24 ) and ( 25 ) show that the mechanism will be stiffly positioned if it has n=6 links, i.e. the Degrees-Of-Freedom of the platform will be zero.

C.2. Choosing Manipulator Dimensions

Dimensions of the manipulator have to be chosen to satisfy several contradictory conditions:

• small overall size of the mechanism
• large base to provide stability
• small base to avoid singularities due to rotation about a horizontal axis
• short link lengths to provide stiffness and small positioning error
• large workspace requires long links

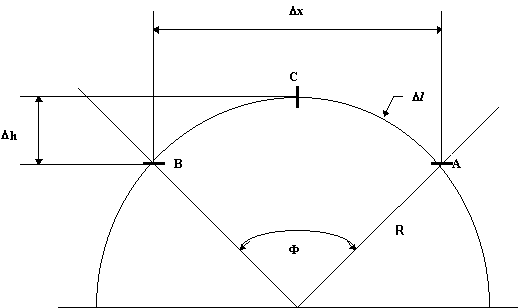
Dimensions are calculated taking as a main requirement, the anticipated trajectory of the manipulator. The tracking platform should follow a trajectory whose shape is close to a circular arc of the radius R = 10 cm, maintaining constant distance and relative orientation with respect to the markers on the heart surface, as shown in Figure 6. The angle spanned by the trajectory is F = 90º,

Figure 6. Trajectory is approximated with an arc from point A, through point C, to the point B.

Figure 7. Stewart Platform with fixed actuators relative to the heart and platform trajectory (marked with a dotted line)

Figure 8. Approximate dimensions of the Stewart Platform can be calculated choosing margin angles a and b. Platform is observed in neutral position and at the end-point of the trajectory.

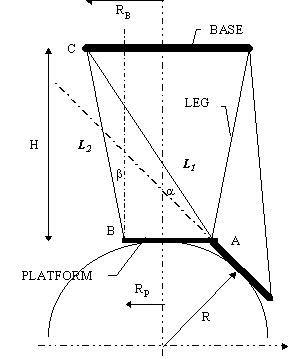
In order to avoid singularities, a security margin of 15º between the platform and the links is taken. The dimensions of the actuator are calculated from there using simple trigonometry. Figure 8 represents a simplified drawing of an SP. The pla tform is observed in two positions: in the "neutral" position at the lowest point of the trajectory (point denoted with B in Figure 8), and at the end-point of the trajectory (point A). At the point C, where lines L₁ and L₂ intersect, the lower joint of a link should be placed. Taking platform radius to be r_p= 3 cm, base radius and height of the platform in neutral position can be calculated. From these values it is easy to derive link lengths and o btain, through simulation, actual margin angles. Calculated parameters of the SP is given in the following table:

The manipulator with these dimensions looks tall and slender, with height to width ratio greater than 3:1. That means that oscillations might occur if the links are not rigid enough. The manipulator would be shorter and stiffer if the requirements for the platform rotation about the horizontal axis are weakened.

C.3. Effect of Finite Actuator Step Length on Positional Accuracy

Due to the finite accuracy of the actuators, joint misplacement and other unmodelled effects, the actual platform position will differ from the commanded one. Closing a feedback loop in the control system decreases the systemati c error due to differences between the ideal and the real model. Since the error due to the finite length of the actuator step cannot be eliminated, we need to investigate the effect of this finite length on the platform positional accuracy. To evaluate p ositional accuracy, we simulate an SPFA moving along a chosen trajectory and calculate maximal position errors and maximal orientation error. Sensitivity of the pose, meaning both position and orientation, is defined as the difference between comm anded and achieved positions. Translation and rotation are treated differently because of the different nature of their contribution to the joint error.

The position error is distance of the center of the platform from the expected position. The rotation error is calculated in the following manner. A camera is positioned in the center of the platform. A point in the space is imaged by two cameras, one on the error-free platform, and one on the platform with errors. The error is calculated as the distance between the perspective projections of the point. The camera focal length is set to f = 1cm. The idea behind this way of measuring the error is that it includes both the position and the orientation error in the same quantitative value. The rotation error is also expressed in degrees, by calculating the angle between the platform normal in the desired and actual position s.

The shape of the base and platform is and the sensitivity is calculated for three configurations. The shapes of the base and the platform are chosen to vary from regular hexagon, through irregular hexagon to a triangle. Other parameters of the manipul ator are as calculated before for the trajectory in Figure 6:

r_b = 7.6 cm Radius of the base

r_p = 3.0 cm radius of the platform

H = 26.0 cm height of the platform in neutral position

The results for the actuator step size of 0.1 mm and for three different configurations of the manipulator, are given in the following table:

As we can see from the above table, when both base and platform are triangle shaped, the accuracy is the greatest, but the required travel of the actuator is the longest. Although a triangular base triangular platform yields the highest positional acc uracy, it is unattainable in the real world since it requires that two actuators (which have finite size) be attached to the same point of the base. Configuration 2 (the semi-hexagonal base and triangular platform) is the best compromise since it allows r eal actuators of finite size to be placed close together. On the other hand, double U-joints permit two vertices of the platform to be essentially at the same point [Fitcher86].

The above method of error measurement is somewhat random, because the maximal error in the simulation depends on the actuator step size and on the initial heights of the actuators. Another way of presenting accuracy of the Stewart Platform manipulator is to calculate the "average" error for a given pose. In the Figure 9 are shown the averaged positional and rotational errors. The manipulator with semi-hexagonal base and triangular platform is used for the calculation.

The errors in position and orientation of the platform caused by an infinitesimal displacement of each link are calculated first, and then averaged in a certain way to give one value. The Jacobian tells us how much the platform will move if the actuato rs move by an infinitesimal amount:

and similarly, the orientation errors are averaged:

The graphs show that the positional error does not change much when the platform is inclined with respect to the base, but the rotational error increases with the inclination angle.

C.4. Practical Considerations

C.4.1. Actuators

The Stewart Platform with Fixed Actuators (SPFA) needs linear actuators. Linear motion can be obtained from linear electrical motors, or by converting rotary to linear motion. The low-end version of the manipulator would benefit from the rotary stepper motors, which are readily available, cheap and relatively easy to control using discrete steps. That also means that the manipulator can be actuated open loop, if the position of the actuator is estimated by a product of the number of motor steps and the step size. If a rotary motor is used as an actuator, some kind of transmission from rotary to linear motion is needed. Rotary motion is usually converted to linear movements using the rack-and-pinion or the ball-screw transmission.

The advantages of the rack-and-pinion over ball-screw transmission are:

• allows easy adjustment of the rotary-to-linear transformation constant by choosing different pinion radius
• takes less space in vertical direction because the motor can be placed perpendicular to the rack
• more appropriate for higher speeds, if the pinion radius is appropriately chosen
• better efficiency

The advantages of the ball-screw over the rack-and-pinion transmission are:

• zero backlash
• the platform stops in the case of power shutdown

Whether the linear or rotary motors are used, a spring is needed to oppose the gravity, since the actuators will be used in the vertical direction. The spring length should be at least three times the travel of the actuator, which would considerably in crease the dimension of the device. This problem could probably be solved if the ball-screw mechanism is employed, but at the cost of having a slower and less efficient system.

The following calculations are performed to verify if the required velocities and accelerations could be achieved if some off-the-shelf rotary motors are used. The load of 2kg is supported by six links and the average load per link is taken to be one s ixth of the mass, so m = 1/6·2kg = 0.33 kg. The travel of the actuators is h = 5 cm, the root-mean-square speed of the linear actuator is V_rms = 1 m/s, root-mean-square acceleration is a_rms = 20m/s² and the transmission efficiency of the rotary-to-linear conversion is h = 60% . A DC servo motor AEROTECH Model 1050 has the rotor inertia J_m = 5.7e-05 kg m². Then, the optimal radius of the rotary-to-linear conversion pinion would be

The radius is then chosen to have some standard value, r = 0.5·1" = 12.7 mm, which yields the root-mean-square angular velocity w _rms = V_rms/r = 79 rad/s= 752 rpm, and the root-mean-square angular acceleration a _rms = a_rms/r = 1606 rad/s². The required torque can then be calculated from the formula:

This gives the result of T_rms = 0.23 Nm which is less than 0.30 Nm specifications for the given motor at the given angular velocity. This simple calculation does not intend to estimate precisely the values to be achieved, but rather serves as an indicator of the feasibility of the device.

C.4.1. Joints

The end of links should be connected to actuators and platform using universal joints. Universal joints (Hooke, U-joints, gimbals) give a much greater range of motion than ball-and-socket joints [Fitcher86]. That requires additional cylindrical joint i n the link to achieve the required five degrees of freedom per link. For the manipulator parameters calculated before, simulation showed that the ball-and-socket joints at the platform should have a workspace of a 155° cone, and those at the base should s pan a cone of 50°, values that are usually not associated with this type of joints. Double U-joints, as shown in [Fitcher86], are used to make platform ends of two links coincident. That means the geometry of the platform will be triangular rather than he xagonal, which is a more accurate manipulator configuration.

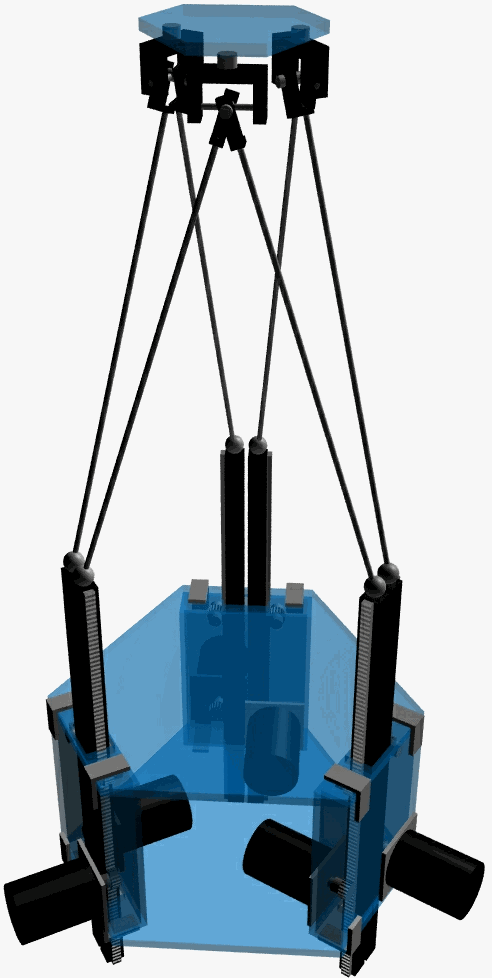
The CAD model of the Stewart Platform with Fixed Actuators prototype is shown on the image to the left. The stepper motors are coupled to racks and pinions elevating the U-joints at the lower end of the links. The U-joints are represented by spheres fo r simplicity. The upper ends of three pairs of links are connected to a double, single-sided U-joint. The manipulator will eventually be used in the upside-down position.

Figure 10. The CAD model of the Stewart Platform with Fixed Actuators, using the dimensions calculated in this paper (CAD design by Joshua Targownik).