A platform manipulator for the CABG surgery device would have to be able to move actuated surgical instruments and a camera, fast and precise enough to follow the heart movements and conform to safety requirements at the same ti me. Requirements for the manipulator design are:
 |
As a possible actuating system, three options are investigated: Cartesian gantry, robotic arm and Stewart Platform-type manipulator. The first option is Cartesian 3-DOF gantry device (X-Y-Z table) placed over the chest cavity. Attached to the end poin t would be a small 3-DOF wrist that would orient the surgeon's tools. While this is conceptually the simplest device, we believe it may be difficult to actuate it with the required accelerations needed to null out the motion of the heart. The second opt ion is a more conventional robotic arm with 6-DOF. This could be placed over the chest cavity from a distance, and could be more massive and stable. However, the accuracy and actuation velocities for this approach may also be prohibitive. Robotic arms a re widely used in stereotactic neurosurgery because of their large workspace, but they are actuated at very low speeds.
Although a gantry is conceptually the simplest device, a Stewart Platform (which is referred to in the text that follows as an SP) is chosen because of its inherent advantages [Merletwww], [Fitcher86] over serial link manipulators, which are des cribed below. It is configured as a platform connected to its base by 6 links whose length can change, offering controllability of 6 degrees of freedom. Being a parallel link manipulator, its positioning accuracy is better than the accuracy of individual actuators, the stiffness is high because forces are distributed to 6 links in the longitudinal direction and required actuating forces are small due to the light load. For instance, in serial link manipulators like a gantry or a robotic arm, the first mo tor has to support the weights of all the motors actuating the succeeding links. The drawbacks of the Stewart Platform-type manipulator are considerably smaller workspace and the existence of singular positions. The singular positions are the positions in which the mechanism cannot be controlled any more. An SP can reach these in many different ways, but there are apparently two different types of singularities. One appears when the platform gets into the same plane with one of the links. Another occurs w hen the platform rotates 90° about an axis perpendicular to it [Fitcher86].
 |
Stewart Platforms (SP) are commonly used in flight simulators and for positioning heavy tools, for instance in orthopedic surgery [Brandt97]. Extendible links are implemented there as hydraulic pistons, giving very high f orces and stiffness but low velocities. Several other configurations are used in order to achieve larger workspace or higher speeds. In order to achieve higher speeds, a mechanism called a Stewart Platform with Fixed Actuators (which is referred to in the text that follows as an SPFA) is proposed. An SPFA has linear actuators fixed on the base moving links of constant length. The advantage of this approach is that power is not used to move heavy actuators but only lightweight links, and the actuators can be firmly fixed to the base to dampen high acceleration movements. The drawback is a smaller workspace in comparison with a standard SP, for the same travel of the linear actuators. Also, forces acting on the actuator have a perpendic ular component, whereas forces exerted upon standard SP actuators have only a longitudinal component.
Linear motion of the required velocity and acceleration can be achieved either by using linear electromotors or rotary electromotors with a converter from rotary to translatory motion. Rotary electromotors are relatively cheap and readily availa ble, but their disadvantages are low transmission efficiency (around 60%) and mechanism inaccuracies introduced with each new moving part. Conversion from rotary to translatory motion is usually performed by ball-screw transmission or rack-and-pinion tran smission. The ball-screw has a useful safety feature that in the case of a power shutdown the mechanism will be held in place. The rack-and-pinion transmission has better efficiency and is better suited for the high speeds required for this application. < B>Linear electric motors, on the other hand, are fast and their energy is directly transformed into linear motion.
It is interesting to note that the actuators need not act linearly: movement of an actuator along any trajectory, an arc for instance, would make possible the same motion of the platform, although the closed form inverse kinematics would not be possible in general case.
B.2. Inverse and Forward Kinematics
 |
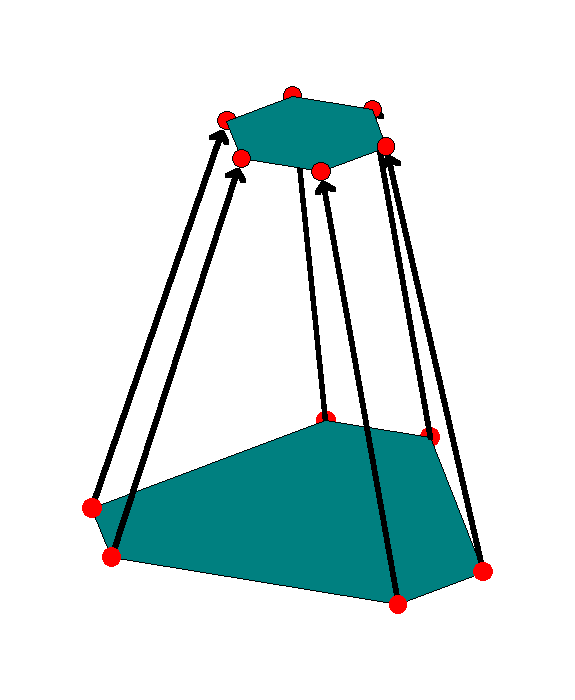
Positions of the base and the platform are uniquely defined by the coordinates of the six joints that connect them with links. The six points are usually chosen to form an irregular hexagon in one plane, although, in general, th ey can be anywhere in the space. Vertices of the platform are defined by six vectors relative to the platform coordinate system {P}, and the base is defined relative to the base coordinate system {B}. Using homogeneous coordinates, the vecto r Ppi=(pxi,pyi,pzi,1)T describes the position of the joint connecting the platform to the i-th link, with respect to {P}. Vector Bbi=(bxi,byi,bzi,1)T , describes the position of the i-th actuator.
The platform is supported by links of constant length li, and the links attached to the actuators that can change the height hi, as shown in Figure 3.
The base is considered to be stationary, and a transformation is needed to find coordinates of the platform with respect to base coordinate system:
|
B pi = R Ppi |
where R is a 4x4 homogeneous transformation matrix:
|
|
( 2 ) |
 |
where Rot denotes a rotation matrix and T a translation vector. The convention in this text is such that if no referent system is specified, the default is the base coordinate system.
The base and the platform are usually designed as an irregular hexagon positioned in the x-y plane and symmetric with respect to the y-axis as in the Figure 4. The distance from the platform coordinate center to each platform joint (P1 - P6 ) is equal to the radius of the platform rP, and the shape is determined by an angle q P, between the first two joints. Similarly, the shape of the base and the coordinates of base joints (B1 - B6) are determined by rB and q B. Now, denoting the angle between PPi and x axis by l i (see Figure 4), and between BBi and x axis by L i for i=1,2,...,6 , we obtain:
|
|
|
|
|
( 4 ) |
As defined before, vector Ppi=(pxi,pyi,pzi,1)T describes the position of the i-th platform joint with respect to platform coordinate system and Bbi=( bxi,byi,bzi,1)T describes the position of the i-th base joint with respect to the base coordinate system. They can be written as:
|
|
( 5 ) |
|
|
( 6 ) |
for i=1,2,...,6.
Parallel and serial link manipulators have some dual properties: serial manipulators have high speed, large workspace, low precision and stiffness, whereas parallel manipulators have low speed, small workspace, high precision and stiffness. Their mathe matics shows similar properties: it is straightforward to calculate forward kinematics of a serial link manipulator if all the joint positions are known, but inverse kinematics (find joint positions for known end-effector pose), in general, is obtained us ing iterative methods. Conversely, inverse kinematics calculation is straightforward for parallel link manipulators, when the end-effector position is given, and iterative methods are used for calculation of forward kinematics.
 |
The inverse kinematics for SPFA can be formulated so as to determine required actuator heights for a given pose of the platform with respect to the base. Pose here implies both Cartesian position and orientation. SPFA actuators are consid ered to act linearly in the vertical direction, parallel to the z-axis, in order to simplify the mathematics, although that need not be the case. Actuator trajectory can be arbitrary, which can simplify the mechanics, but the closed form solution would not be possible, in the general case.
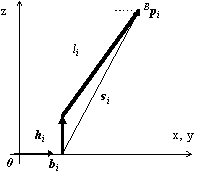
From the Figure 5, if the positions of the actuator position bi, platform joint pi and the length of the link li are known, we have:
|
|
( 7 ) |
|
|
( 8 ) |
This is a simple way to find the height of the i-th actuator. The solution is the point at the intersection of the actuator motion line and a sphere whose center is the platform joint pi and with the radius equal to the link length li (Figure 5). Since there are two intersection points, the solution is not unique, and it even does not exist if the platform joint is too far from the actuator.
The problem of forward kinematics is to determine the pose of the platform with respect to its base, given the actuator heights. The pose is defined by equation ( 1 ), as the dot product of the transformation matrix and the platform joint coordinates. The transformation matrix contains redundant information since its 4x4 elements can be uniquely found from six parameters that control six degrees of freedom. Here, we will choose these six parameters to be: x, y and z translation parameters and
a, b and g roll-pitch-yaw rotation parameters:
|
|
( 9 ) |
Equations ( 7 ) and ( 8 ) define function (G:s® h), and since it cannot be inverted in a closed form, vector s can be estimated by linearizing function G(s(q)) around initial value of the actuator height h, with respect to vector q, using Newton’s method. The following equatio ns will consider only one actuator, so the subscript i will be left out for simplicity.
|
|
|
|
|
( 11 ) |
From equation ( 8 ), we have a derivative of the function G with respect to s:
|
|
( 12 ) |
It is also necessary to determine dR/dq. Since R is a 2-dimensional matrix, and q is an 1-dimensional vector, the derivative will be 3-dimensional. It can be seen as six 4x4 matrices stacked together, the first one is the de rivative of the transformation matrix with respect to the first element of vector q, d R/dq1, the second is dR /dq2, and so on.
The elements of the transformation matrix depend on the translation and rotation. As previously stated, translation is determined by x, y and z values and rotation by roll-pitch-yaw angles
a, b and g. Pose of the platform coordinate system {P} can be obtained by the following sequence of fundamental rotations and translations of the bas e coordinate system {B}:
The resulting homogeneous transformation matrix takes the following form:
|
|
( 13 ) |
where c
a = cos a, sa = sin a. Deriva tives of the transformation matrix with respect to x, y, z, a, b and g are given below:
|
|
( 14 ) |
|
|
( 15 ) |
|
|
( 16 ) |
|
|
( 17 ) |
|
|
( 18 ) |
|
|
( 19 ) |
To summarize, matrix H = dG/dq is a 6x6 matrix whose elements are:
|
|
( 20 ) |
Below is the algorithm for forward kinematics. It takes as input the model of the base b and the platform p, and the heights of the actuators h0. The output is the pose of the platform represented by the transformation m atrix R or the pose vector q.
The algorithm performs iterations, calculating the increment in the platform pose Dq and the link lengths for the new pose h. It terminates when the difference Dh between the calculated and the desired actuator positions drops below a small number e.
Step 8 involves implicit inversion of matrix H. If the matrix is nearly singular, that means the position is close to the singular position and special attention is necessary.
Equation ( 10 ) gives the relationship between the infinitesimal changes of actuator heights and the changes in pose. Dividing both sides of that equation by an infinitesimal time period gives a relationship between actuator velocities and the platform translational and rotational velocities. The inverse of matrix H is also called the Jacobian matrix:
|
J = H -1 |
( 21 ) |
|
|
( 22 ) |
This method is general in the sense that all the joints of the platform or actuators on the base need not be in one plane. This fact is useful if the joint coordinates are estimated after the manipulator is manufactured, and new, re-calibrated values a re used for the forward kinematics.
It is important to note that the solution for forward kinematics is not unique. It is not necessary to have actuator height feedback if feature space feedback is used and approximate position of the actuators is known. However, if the manipulator enter s singular position, platform pose cannot be calculated with confidence from actuator heights.
For the standard configuration of a Stewart Platform, faster methods for forward kinematics exist when joints are coplanar [McAcree96]. These methods involve inverting a 3x3 instead of a 6x6 matrix, so that they can be written in the closed form. I am not aware of such a method that can be applied to a Stewart Platform with Fixed Actuators.